Ergebnis 1 bis 11 von 11
-
12.10.2012, 12:24 #1TheMan


Komplexe Zahlen Verständnisfrage
Hey Leute,
mal eine kleine Frage, und zwar stehe ich bei folgender Aufgabe auf dem Schlauch.
Komplexe Zahlen addiere ich ja wie folgt
Code:z1 = x1 + jy1 z2 = x2 + jy2 z1 + z2 = (x1 + jy1) + (x2 + jy2) = (x1+x2) + j(y1+y2)
Jetzt zu meiner Frage, gibt mir die Aufgabe quasi diesen dick markierten Zwischenschritt an?
Sodass ich nur noch die beiden Teilstücke in den TR eingeben muss, was dann
wäre = 1,9318 + j0,5176
und dieses Ergebnis dann halt in die Polardarstellung überführen?!
Lieben Gruß
The Man
-
-
13.10.2012, 00:13 #2Issomad


AW: Komplexe Zahlen Verständnissfrage
Ähm, der imaginäre Teil wird mit i bezeichnet, nicht mit j ... Das gäbe dicke Formfehler bei einer Arbeit ...
-
13.10.2012, 00:28 #3Kimmel


AW: Komplexe Zahlen Verständnissfrage
-
13.10.2012, 00:42 #4Issomad


AW: Komplexe Zahlen Verständnissfrage
Ja, anscheinend ist die Unart in der E-Technik so ...
Vielleicht hilft das Video auf dieser Seite weiter:
Komplexe Zahlen in kartesischen Koordinaten und Polarkoordinaten | ET Tutorials
Also im Endeffekt: Die Länge von Vektor z * e^jφ
wobei φ der Winkel zwischen der Real-Achse und dem Vektor ist ...
-
13.10.2012, 01:05 #5TheMan


-
13.10.2012, 04:08 #6Issomad


-
13.10.2012, 11:58 #7TheMan


-
13.10.2012, 14:17 #8OmegaPirat

AW: Komplexe Zahlen Verständnissfrage
Mathematiker schreiben auch nicht komplexe Zahlen mit dem i, sondern als Tupel auf dem eine additive und multiplikative Verknüpfung entsprechend definiert sind.
Ansonsten sind sowohl das i als auch das j in den angewandten Fächern weit verbreitet.
Du darfst in der Polarform nicht das i oder j im Exponenten vergessen.
Also ich würde schreiben
2*e^(pi/12*j)
-
13.10.2012, 14:54 #9
-
13.10.2012, 22:34 #10TheMan


AW: Komplexe Zahlen Verständnisfrage
@OmegaPirat
@Issomad
@Kimmel
Muss leider einen Doppelpost machen da ich noch eine kleine Frage habe.
Bei quadratischen Gleichungen im Komplexen bestimme ich ja die Werte unterhalb der
Wurzel wie folgt

Auf z1 und z2 natürlich noch 7/2 j draufrechnen
Aber wie ist das, wenn ich unter der Wurzel nur einen negativen Reellen Teil habe?
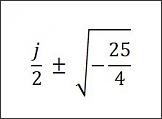
-
14.10.2012, 10:18 #11OmegaPirat

AW: Komplexe Zahlen Verständnisfrage
Das ist nicht viel anders. In diesem Fall ist der Imaginärteil unter der wurzel 0.
Du kannst also schreiben
Wurzel(-25/4)=Wurzel(-25/4+0i)
Der Betrag von -25/4+0i ist
Wurzel((25/4)²+0²)=25/4
Der Winkel ist pi
Du solltest dir übrigens angewöhnen in Bogenmaß zu rechnen und zu denken. Das Gradmaß ist sehr unhandlich und es ist auch unüblich hier in Gradmaß zu rechnen.
Ähnliche Themen
-
komplexe Elektrotechnik: Hey Leute, ich bin momentan ein paar E-Technik Aufgaben am rechnen, und wollte Fragen ob folgendes richtig ist. Anbei Aufgabe sowie Lösung... -
Schritte zählen!!: Postet mal wie viele Schritte ihr immer lauft und wie se zustande gekommen sind. Bin heut mit meinen Kids spazieren gewesen. Hat satte 1617... -
Komplexe Zahlen Frage: Moin kann mir jemand helfen und mir diese Gleichung eines Kreise auflösen/erklären? |z-6-4j| ______ =3 |z+5| verstehen tu ich noch... -
Wer von euch hat Komplexe?: :D ja schön das ich wieder beginnen darf.... sagen wir mal so es gibt sicherlich gescheitere Menschen als mich... aber ich habe deswegen nicht... -
Nür für Wii GEZ zahlen?!: Hallo allerseits. Ich möchte meinen TV abmelden, da ich wirklich GARNICHT mehr fernsehe. Jetzt hab ich auf der GEZ Seite gelesen: "Bitte...








NSO hat wohl eines der spannendsten Angebote! Für jede, bis zum 1.12 abgeschlossene oder verlängertes Online Abo, bekommt ihr per Code dasselbe...
Nintendo Switch Online Dienst