Ergebnis 1 bis 20 von 121
Thema: Der Mathe Nachhilfe Thread
-
22.10.2014, 16:25 #1Mr. Miyagi


Der Mathe Nachhilfe Thread
Moin Moin Mathegenies und die, die es werden wollen! (so wie ich)
Ich habe des Öfteren hier in meiner Mittelstufen- und Abizeit Fragen bezüglich Mathe gestellt und mir wurde (überraschender) Weise immer gut und verständlich bei dem jeweiligen Problem gehoofen.
Überraschender Weise, weil ich nicht so viel Hoffnung hatte, dass mir in einem Forum für Unterhaltungselektronik, etc so gut in Sachen Mathe geholfen wird. Dann wohl eher in einem Schulforum oder ähnlichem.
Aber weil nun mal Forumla the one and only Forum für mich ist Und sich hier wohl viele kluge Köpfe rumtummeln. Bin ich garnicht mal an der falschen Adresse.
Und sich hier wohl viele kluge Köpfe rumtummeln. Bin ich garnicht mal an der falschen Adresse.
Jedenfalls dachte ich mir, da es außer meinen, viele andere Frage Threads gab, erstelle ich einen für alle.
Ich habe mir vorgestellt, dass man hier eben Fragen posten kann und wir uns gegenseitig dabei helfen. Eben wie bei einer Mathenachhilfe.
Vielleicht kann auch ich mal meinen Teil dazu beitragen, wenn es z.B um Stoff aus der Mittelstufe und dem Abi geht!
Dann fang ich auch direkt mal an. Ich studiere seit kurzem Bauingenieurwesen und bin z.B. ein wenig überfordert, was so Kleinigkeiten bei der Schreibweise angeht.
Darum solls aber grad nicht gehen. Ich habe eine Verständnisfrage zu folgender Aufgabe:
x ist Element aus den ganzen Zahlen Z
Gesucht ist die Menge aller x Element Z, welche die Gleichung löst.
5*x + 3 = 2*x^2
Gelöst werden soll mit der quadratischen Ergänzung.
Wenn ich das nun löse bekomme ich am Ende nach dem Wurzel ziehen
x1 = - (25/16) + (7/4) -> 3\16
x2 = - (25/16) - (7/4) -> 53/16
Nun will ich die Lösungsmenge bestimmen. Da stellt mir sich die Frage, ist das nun eine leere Menge?
Es ist von x Element aus Z, also den geraden Zahlen die Rede. Die x Werte sind jedoch Brüche.
Was heißt das nun? Hab ich mich verrechnet, ist das nun die leere Menge oder was anderes?
Hab noch nicht ganz verstanden, wann es sich um leere Mengen handelt und wann nicht.
-
-
22.10.2014, 16:33 #2Octavian
AW: Der Mathe Nachhilfe Thread
x=3 ist eine Lösung. Du hast dich verrechnet.
-
22.10.2014, 18:07 #3Mr. Miyagi


AW: Der Mathe Nachhilfe Thread
Ich habe keine Ahnung was ich angestellt hab. Aber habe es gerade wieder gerechnet und habe auch 3 raus.
x1 ist 3 und x2 ist -1/2
Wie schreibe ich das nun auf? Habe mit sowas Probleme, weil ich das nie in der Schule gelernt habe.
x2 trifft ja nicht auf die Bedingung x aus ganzen Zahlen zu.
Wäre L = {x Element Z | 3 \ -1/2 } richtig formuliert?
Kommt mir irgendwie falsch vor. Ich muss ja sagen dass 3 eins der x Elemente aus Z ist und -1/2 nicht.
-
22.10.2014, 21:59 #4Kimmel


AW: Der Mathe Nachhilfe Thread
Wenn du das ganz formal haben möchtest (ich habe nicht nachgerechnet, ob eure Lösung stimmt):
http://www.matheboard.de/latex2png/latex2png.php?L%20=%20\{%20x%20\in%20\mathbb{Z}%20\%20|%20\%205x%20+%203%20=%202x^2%20\}%20=%20\{%203%20\}
-
22.10.2014, 23:23 #5Calc


AW: Der Mathe Nachhilfe Thread
Die Frage ist konkret was du auffschreiben willst. Möchtest du die Bedingung auffschreiben, dann ist die Formale Schreibweise von Kimmel {x € Z | 5x + 3 = 2x^2} richtig. Möchtest du nur noch die Lösungsmenge angeben, dann reicht L = {3}. Deine ausgerechneten -1/2 musst du nicht mehr angeben, weil du schon in der Definition gesagt hast, dass x Element der Ganzen Zahlen ist (dafür steht ja das Z). Demnach ist -1/2 ganz einfach nicht Teil der Lösungsmenge weil es keine ganze Zahl ist.
-1/2 ist also eine "Pseudolösung", die zwar deine Quadratische Gleichung (in einem anderen Anwendungsfall) auflösen kann, aber deine Bedingung Teil der ganzen Zahlen zu sein, nicht erfüllt. Deshalb musst du sie weder aufschreiben noch explizit in der Lösungsmenge ausschließen. Was du machen kannst ist bei deinem Rechenweg an dieser "Pseudolösung" einen Blitz zu malen und direkt daneben zu schreiben, dass x nicht Element der ganzen Zahlen ist und daher keine Lösung darstellt.
p.s. zu deiner Frage im ersten Post: Gemäß den Fall es wären nur Brüche herausgekommen, wäre die Lösungsmenge die Leere Menge.
-
25.10.2014, 15:35 #6Mel C

-
25.10.2014, 16:26 #7Octavian
AW: Der Mathe Nachhilfe Thread
Ich denke das wird im Rahmen eines technischen oder wirtschaftlichen Studiengangangs gelehrt.
Isoliert gesehen ist das Lösen solcher Gleichungen sinnlos, in allen anderen Fächern brauchst du das allerdings ständig. Man schafft mit den Grundlagen in Mathematik eine Basis für alle anderen Bereiche in denen man darauf zurückgreifen muss.
-
25.10.2014, 20:11 #8Gilligan


AW: Der Mathe Nachhilfe Thread
-
25.10.2014, 20:44 #9Mr. Miyagi


AW: Der Mathe Nachhilfe Thread
Nun ja solche isolierte Aufgaben ohne jeglichen Hintergrund dienen nun mal dazu, um es mit den Worten unserer Dozenten zu wiederholen, das mathematische Handwerk zu lernen. Nach 100000 mal durchrechnen versteht man sein Handwerk selbst im Schlaf.
Und sobald dies der Fall ist, ist man bereit das erlernte Handwerk mit anwendungsbezogenen Thematiken der Physik oä. aufzufüllen.
In meinem Fall passieren diese beiden Prozesse parallel. Denke dass es in jedem anderen Studiengang genau so ist.
-
26.10.2014, 18:35 #10Mr. Miyagi


AW: Der Mathe Nachhilfe Thread
(Konnte nicht mehr editieren, bitte Doppelpost zusammenfügen)
Jetzt hab ich in der Ungleichung (x^2) +1 > 6*x mit der quadratischen Ergänzung die X-Werte berechnet. X1 = (Wurzel aus 8) + 3 und X2 = -(Wurzel aus 8) +3
folgende Gleichung aufgestellt:
(x-x1)*(x-x2) = (x^2) -6x +1 > 0
D.h. (x-x1)*(x-x2) > 0
Daraus schließt man , dass die beiden Klammern entweder positiv oder negativ sein müssen damit größer 0 rauskommt.
Hier wende ich nun die Fallunterscheidung an:
1. Fall
(x-x1) > 0 und (x-x2) > 0
X > x1 und x > x2
2. Fall
(x-x1) < 0 und (x-x2) < 0
X < x1 und x < x2
Aus Fall 1 folgt, dass x größer x1 ist (Wurzel aus 8 + 3) und aus Fall 2, dass x kleiner x2 ist -(Wurzel aus 8 + 3)
Meine Frage ist nun wieder. Wie schreibe ich nun korrekt auf, dass x Element aus R kleiner x2 und/oder (????) größer x1 sein muss.
Ist das ganze überhaupt korrekt ? Leider bin ich noch sehr unsicher was das angeht. Z.B. weiß ich noch nicht genau ob und wann ich ne Fallunterscheidung machen muss und wann nicht...
Achja, das war ne ganz schöne Schreiberei. Wie erstelle ich denn solche Bilder mit den mathematischen Zeichen am PC @Kimmel ?
-
26.10.2014, 19:40 #11Kimmel


AW: Der Mathe Nachhilfe Thread
Du hast dir vermutlich erst http://www.matheboard.de/latex2png/latex2png.php?x^2%20+%201%20=%206x angeschaut (was vollkommen in Ordnung ist).
Sei http://www.matheboard.de/latex2png/latex2png.php?f(x)%20=%20x^2%20-%206x%20+%201. Die Frage ist ja, wann http://www.matheboard.de/latex2png/latex2png.php?f(x)%20%3E%200 ist.
Nun haben wir ein Polynom 2.Grades vor uns. Daher ist entweder
(i) zwischen den beiden Nullstellen http://www.matheboard.de/latex2png/latex2png.php?f(x)%20%3E%200
oder
(ii) links von der kleineren Nullstelle und rechts von der größeren Nullstelle.
Wir stellen fest, dass http://www.matheboard.de/latex2png/latex2png.php?f(3)%20%3C%200 gilt, weswegen (ii) gilt (die 3 befindet sich zwischen den beiden Nullstellen).
Damit haben wir
http://www.matheboard.de/latex2png/latex2png.php?\mathbb{L}%20=%20\{%20x%20\in%20\mathbb{R}%20\%20|%20\%20f(x)%20%3E%200%20\}%20=%20\{%20x%20\in%20\mathbb{R}%20\%20|%20\%20x%20\notin%20[%20-\sqrt{8}+3,%20\sqrt{8}%20+3]%20\}
Ich benutze diesen Formeleditor:Achja, das war ne ganz schöne Schreiberei. Wie erstelle ich denn solche Bilder mit den mathematischen Zeichen am PC @Kimmel ?
http://www.matheboard.de/formeleditor.php
-
26.10.2014, 21:01 #12Mr. Miyagi


AW: Der Mathe Nachhilfe Thread
Sind i und ii deine zwei Fälle? Und wie bist du auf f(3) < 0 gekommen?
Also sind meine zwei Fälle und die Schlussfolgerung falsch?
Ich versteh deine Lösung noch nicht ganz.
-
26.10.2014, 21:22 #13Calc


AW: Der Mathe Nachhilfe Thread
Ich würde es einfach so machen:
(x^2) -6x +1 > 0
=>
(x^2) -6x > -1 | Quadratische Ergänzung (p/2)^2 also (6/2)^2 = 9 auf beiden Seiten addieren
x^2 - 6x + 9 > 8 | Binom
(x-3)^2 > 8 | Wurzel
|x-3| > Wurzel(8)
Fallunterscheidung
I. Fall
x-3 > 0 => x > 3
II. Fall
x-3 < 0 => x < 3
Lösung I. Fall
x-3 > Wurzel(8)
x > 3 + Wurzel 8 (bedingung x > 3 erfüllt)
Lösung II. Fall
-(x-3) > Wurzel(8)
-x+3 > Wurzel(8)
-x > -3 + Wurzel(8)
x < 3 - Wurzel(8) (bedingung x < 3 erfüllt)
=> x ist Element von (-unendlich, -Wurzel(8)+3) U (wurzel(8)+3,unendlich)
(Äquivalent zu dem was Kimmel geschrieben hat x ist Nicht Element von ...)
-
26.10.2014, 21:51 #14Kimmel


AW: Der Mathe Nachhilfe Thread
Ja, der eine Fall schließt den anderen aus.
Ich habe mir einen Wert zwischen den beiden Nullstellen gesucht und ihn dann in die Funktion eingesetzt. Der Rest ist dann rechnen.Und wie bist du auf f(3) < 0 gekommen?
Das habe ich nicht gesagt.Also sind meine zwei Fälle und die Schlussfolgerung falsch?
Du kannst dir alternativ auch Calcs Lösung anschauen, die über das Rechnen mit Ungleichungen und lösen dieser geht. Sie ist für dich vielleicht etwas intuitiver.Ich versteh deine Lösung noch nicht ganz.
Wenn dich aber mein Lösungsweg interessiert, dann kann ich mehr dazu schreiben.
-
26.10.2014, 22:17 #15Mr. Miyagi


AW: Der Mathe Nachhilfe Thread
Eure Lösungen unterscheiden sich am Ende etwas oder?
Kimmels sagt ja am Ende aus, soweit ich das jetzt verstanden hab, dass alle x Werte aus R gemeint sind, wobei die X Werte die Eigenschaft haben nicht Wurzel(8) + 3 und -Wurzel(8) + 3 zu sein. Da diese keine Elemente sind?
Und Calcs sagt aus das x aus R | (Alle Werte von - unendlich BIS -Wurzel(8)+3 vereinigt mit den Werten ab Wurzel(8) +3 bis +unendlich) gemeint sind.
Kimmels also:
ohne Wurzel(8) +3 und -Wurzel(8)+3
und Calcs:
alles bis (inklusive) -Wurzel(8)+3 und alles ab wurzel(8)+3 bis ins + unendliche
Das ist doch schon ein Unterschied oder nicht?
-
26.10.2014, 22:30 #16Kimmel


-
26.10.2014, 22:34 #17Calc


AW: Der Mathe Nachhilfe Thread
Die Runden klammern bedeuten der Wert liegt nicht mehr im Intervall. Die Eckigen Klammern, der Wert liegt noch im Intervall. D.h bei mir steht es geht von minus unendlich bis -wurzel(8)+3 , wobei -wurzel(8)+3 selbst nicht mehr im Intervall von x liegt. Das was dazwischen liegt, faellt dann raus. Kimmels loesung zahelt auf, welche x Werte nun rausfallen, dort liegt -wurzel(8)+3 noch im Intervall, deshalb die eckigen Klammern.
Die Betrachtungsweise ist als lediglich eine andere. Ich schaue mir an welche x-werte x annehmen kann, kimmel welche Werte nicht von x angenommen werden. Vom einen laest sich aufs andere schliessen.
-
26.10.2014, 23:28 #18Mr. Miyagi


-
26.10.2014, 23:34 #19Kimmel


-
27.10.2014, 00:07 #20Calc


AW: Der Mathe Nachhilfe Thread
Als normalerweise geht es darum die Lösungsmenge zu ermitteln L = x € .... (ohne Mengen Klammern wie Kimmel sagte).
Das R gehört irgendwohin ja, allerdings sollte bereits im Vorfeld ersichtlich sein, dass du von den Reellen Zahlen redest. Normalerweise gibt man dafür ganz formal vor der Rechnung einen Definitionsbereich an (D). z. B. D = R \ {0, 1/4) (Der Definitionsbereich sind die Reellen Zahlen, außer 0 und 1/4 - hat nichts mit deiner Rechnung zu tun, nur ein Beispiel, manchmal kann man sofort sehen das direkte Zahlen nicht im Intervall vorkommen koennen, z. B. weil ein Nenner dann 0 werden würde). Den Definitionsbereich schreibt man Einfach oben Rechts einmal an die Rechnung, in deinem Fall dann D = R. Das muss dann nicht nochmal aufgeführt werden und es reicht die bloße Angabe der Lösungsmenge L.
Ähnliche Themen
-
Nachhilfe gesucht: Hallo, suche einen "Nachhilfelehrer(in) im Raum 58... oder 44... zwecks Verbesserung meiner Mario Kart "Fahrkünste". Stecke auf 8300 - 8500 fest... -
Ehrenamtliche Nachhilfe an der Hauptschule: Moin^^, ich wollte mal nachfragen wa sihr davon haltet kostenlos an der Hauptschule Nachhilfe zu geben. Die Schüler dort machen freiwllig bei dem... -
Kostenlose Mathe Nachhilfe: Hallo Leute, ich bin durch Zufall auf eine Super Seite im Netz gestolpert. Sie besschäftigt bzw. gibt Mathe Nachhilfe, der Clue dabei ist daß es... -
Nachhilfe: Hallo, ich hätte mal eine Frage: Also mein Bruder der 13 Jahre ist und in die 7 Klasse geht hat mich Heute mit seinem Problem angesprochen, ich... -
Kostenlose Nachhilfe im Internet mit Videos!: Hallo, vllt brauch ja wer von euch in Mathe nen bisschen Hilfe. Warum nen Nachhilfelehrer bezahlen, nur weil man mal was nicht verstanden hat?...Und...



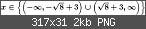



https://www.facebook.com/reel/937965491380172/?mibextid=rS40aB7S9Ucbxw6v:pride:
Die besten und witzigsten Online-Videos